优化器技术演进：统计信息feedback

本文将讲述数据库优化器中，统计信息的feedback机制。对数据库统计信息的概念有基本了解的同学，可以直接跳到第三章进行阅读。

统计信息（statistics）是数据库优化器领域中经久不衰的话题，几乎每年的数据库顶级会议中都会有多篇涉及到统计信息的论文。

在现代数据库中，对于用户传来的SQL，优化器首先为其枚举出不同的执行计划，形成一个搜索空间；然后将收集得到的统计信息（如表的行数、谓词的选择率等）作为输入，在代价模型（cost model）中为不同的执行计划计算出相应的代价。最小代价的计划会被优化器选中，成为最终的执行计划，在数据库执行器中运行。

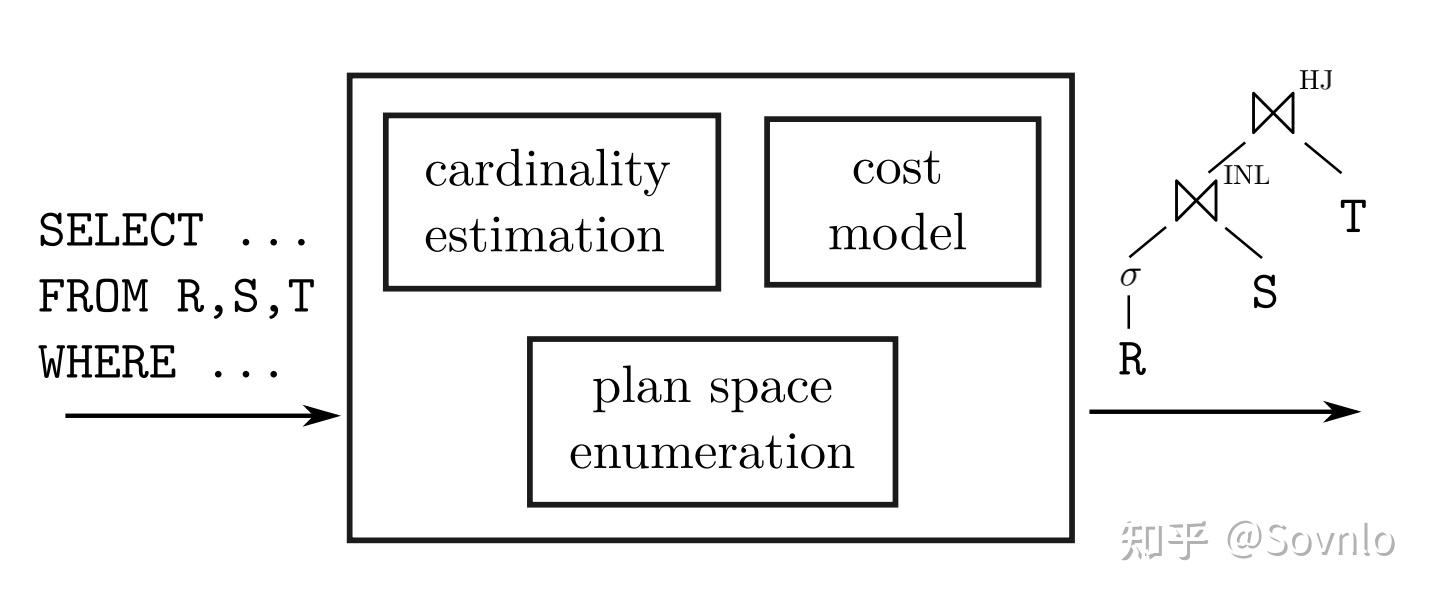
常见的统计信息指标包括但不限于：

1. 表的行数（row count），对于关系R，行数可以表示为
2. 某一列中ndv的数量（number of distinct value），即去重之后元素的数量。
3. 选择率（selectivity），对于某一个过滤条件，被过滤的行的比例。对于关系R上的过滤条件（谓词）p，其选择率可以表示为 .
4. 基数（cardinality），狭义上的基数是指Join / Agg等算子输出的行数。基数估计(cardinality estimation)是数据科学家们研究最多的统计信息问题，几乎成为统计信息的代名词，对于条件为p的Join算子 ， 基数估计常常转化为 的形式来处理。

而为了表示统计信息，数据库科学家们研究出了丰富的表示形式。在数据库学术领域，统计信息的表示形式统称为数据摘要（Synopses），推荐阅读这篇雄文 Synopses for Massive Data:Samples,Histograms, Wavelets, Sketches。

本文关注的统计信息表示形式是最古老、最实用的直方图(histogram)，即柱形图。只表示一列统计信息的直方图，称为一维直方图。一维直方图可以分为以下几种：

1. 频率直方图，用于表示某一列中各个数值出现的频率，其中横轴是一个个按序排列好的区间，每个区间上的柱形称为一个桶（bucket），其高度代表该区间内数据出现的次数（频率）。所有桶的高度之和便是表的行数。频率直方图有等宽、等高之分，

• 等宽直方图，区间大小一致，桶高度不同:

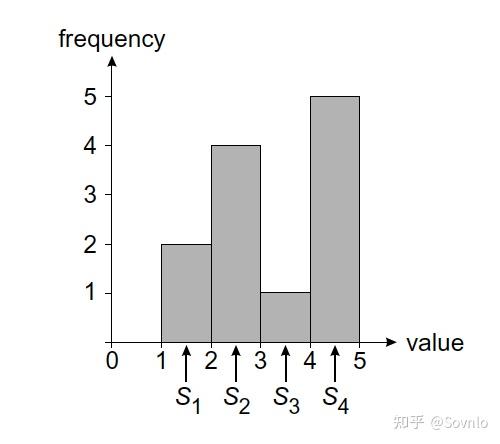
• 等高直方图，桶高度一致，区间大小不同：

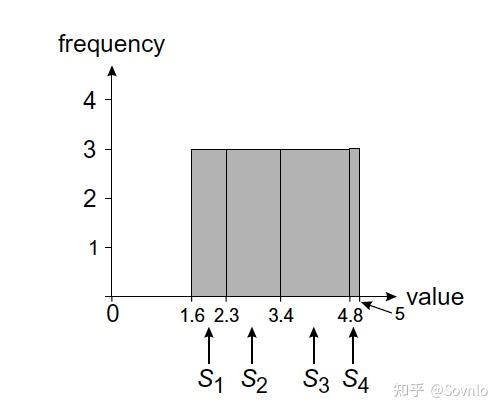
2. TOP-K直方图，在直方图上为列中频率最高的前K个数值，存储相应的频率 ，而其他不频繁出现的数值频率被视为

与一维直方图不同，多维直方图可以表示多个列的频率信息。对于含有d列的高维直方图，原先的一维区间 ，成为了新的高维空间 ，每个桶表示该高维空间内一个区间上的频率值。

从1979年的优化器奠基之作 Access Path Selection in a Relational Database Management System 开始，数据库统计信息的构建一般都遵循着以下几个假设：

时效性假设，即假定过去一段时间内表的数据是不变的，旧的统计信息能准确反映现在时段的数据分布情况。

独立性假设，即假设不同谓词之间概率分布相互独立，互不干预， 对于谓词 ，其选择度满足 。

均匀假设，即假定柱状直方图的每个柱形内部，数据是均匀分布的。例如，表R中A列的真实分布情况如下，其中柱状直方图的横坐标代表distinct value，柱形桶的高度代表该distinct value在表中的数量：

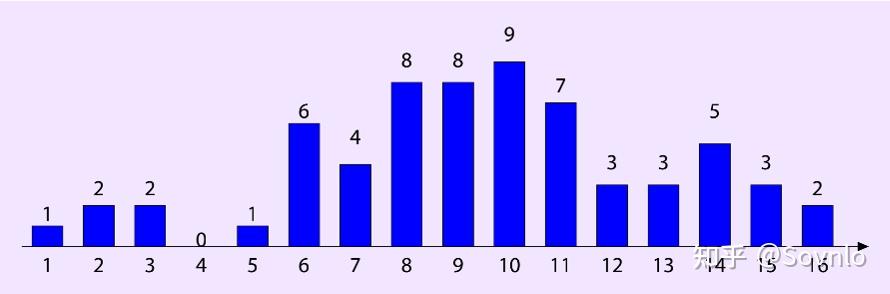
现在我们为A列收集统计信息，其建立如下的等宽直方图，每个桶宽度相同，都覆盖4个distinct value；当我们需要计算满足A=5的行数，首先我们找到区间在[5, 8]的桶，然后根据独立性假设，认为桶内数据是均匀分布的，从而计算出行数 ，与实际结果1有较大误差。

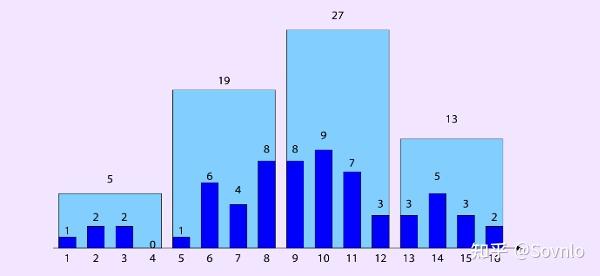
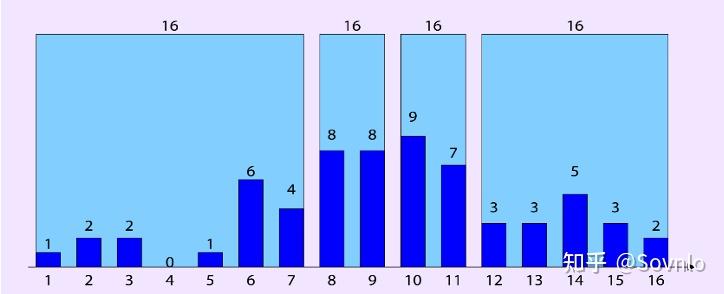
而如果为A列建立如下的等高直方图，每个桶的高度一致。当我们需要计算满足 的行数，假设桶内数据均匀分布，则计算方式为 ，与真实数据 同样存在误差。

包含性原则。对于条件为p的Join算子 ，其选择率往往被粗暴定义为 ，这里隐含一个假设，即对于ndv较小的列而言，每一个列元素都能在ndv较大的列中匹配到相同元素。如果用贝叶斯定理来理解的话，设A事件为R.a列元素发生匹配，B事件为S.b列元素发生匹配，则有 。

在优化器实际运行时，当这些假设出现不成立的情况，统计信息就会出现较大的偏差，给代价估算带来错误结果，进而影响到计划的选取，得到次优的执行计划，给整个数据库的处理性能带来不利。在著名文章 How Good Are Query Optimizers, Really？中提到，底层算子上统计信息估算时的偏差，会在算子间指数级地放大和传递，让最终求得的执行代价差之千里。

为了应对这一问题，统计信息feedback，即在运行时收集统计信息误差，并及时对统计信息进行修正，成为Oracle、Db2等主流数据库厂商采纳的方案。本文将梳理统计信息feedback的发展脉络。

DB2在2001发表文章 LEO – DB2’s LEarning Optimizer，引入了一个完整的、商用的feedback方案"Leo"，整体架构如下：

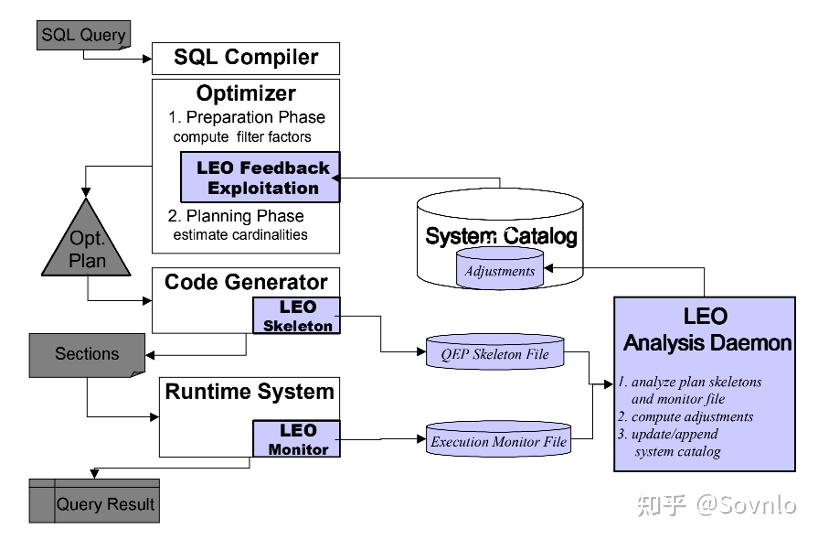
对于用户SQL：

SELECT * FROM X, Y, Z
 
WHERE X.Price >=100 AND Z.City=‘Denver’ 
AND Y.Month=‘Dec’ AND X.ID=Y.ID 
AND Y.NR=Z.NR 

GROUP BY A

Leo优化器处理得到一个执行计划QEP(query execution plan)，称为"skeleton"。相比于一般的执行计划，skeleton可以对每个算子的输入输出行数、执行时间都进行实时监控，并与统计信息估算值进行对比。上述SQL经处理得到的skeleton如下：

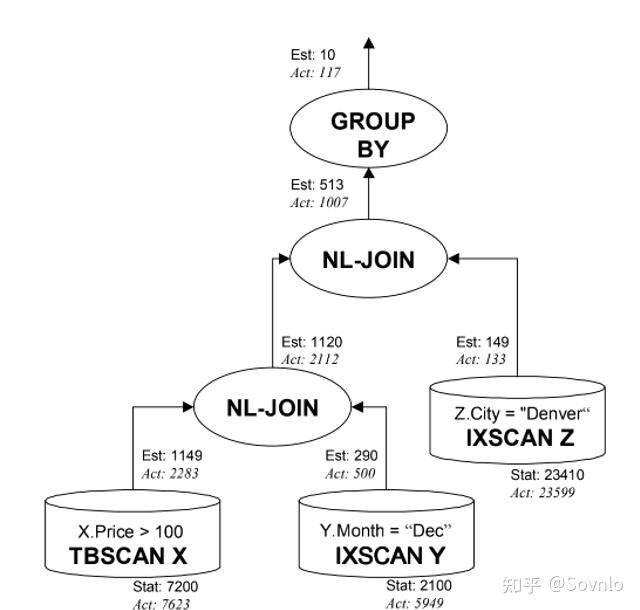
根据收集到的skeleton监控信息，与优化器统计信息估计值对比如下：

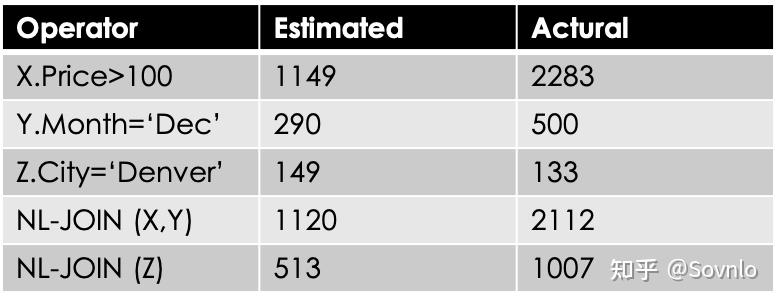
接下来，LEO优化器通过监控分析程序，为出现错误估计的算子，求出一个adjustment数值，来调整算子的选择率，从而修正统计信息带来的误差。

这里需要先引入几个基本概念：

• old_est: 优化器对于选择率的估计值
• old_adj: 优化器用于修正选择率的旧adjustment
• stats：调整前的选择率，old_est /old_adj
• act: 真实的选择率

监控分析程序计算adjustment的过程如下：

1. 首先，监控分析程序后续遍历整个skeleton树，找到最早出现估算错误的算子节点。判断估算错误的依据是， ，即当选择率估计值和真实值差距在5%以上时，认为发生错误。
2. 接着，对于算子（TBSCAN, IXSCAN, FETCH, FILTER, GROUP BY, NLJOIN, HSJOIN等）对比选择度的估计值和真实值， 求出一个adjustment数值：
3. 将求得的adjustment数值存入系统表，作为优化器的输入，在优化时对统计信息进行修正。

上述监控分析程序可以离线，也可以实时执行。实时执行的监控分析，对query响应更快、更灵敏，但是很难保证工程上的准确性。为了不影响程序执行，监控分析由一个优先级很低的线程来处理，仅在数据库负载 较低时触发，并且可以随时被高优先级的线程终止。

adjustment机制有以下几个优点：

1. 可以灵活地关闭和打开feedback功能，（简单地忽略统计信息）
2. 可以将adjustment存入系统表，并通过查阅系统表，得知现有的adjustment的情况，知道哪些谓词、选择度已经被调整过，避免重复调整，或者给予正确的再调整（re-adjustment）
3. 可以对系统表建立一个访问机制，对于adjustment进行人工调优。

Leo优化器规定：用谓词 col < X的adjustment值，来修正 的选择率：

例如，对于skeleton图中的算子TBSCAN X，首先计算谓词price<=100的adjustment ：

接着可以修正得到Price > 100 的真实选择率：

对于join算子 ，Leo将其转为 ，其基数表示为 。这样，adjustment对于谓词选择率的修正，也可以自然地应用到join算子上了。

在统计信息feedback修正方案里，不同于DB2 Leo优化器直接修正选择率，update statistics代表了一种更长期、更直接的修正，即根据算子上监控得出的反馈信息，对直方图进行更新，从而给优化器提供更准确的统计信息参考。

update statistics 可以简单地理解为，通过监控得到某个范围内或某个单点的基数信息，如 或 ，将此信息作为feedback，根据修正算法来直接修正和更新原有的直方图。

首先来明确几个概念。记col=v的频率：f(col=v)=fv，

• 原先的频率值
• 从feedback中收集得到的新频率数值信息
• 排在topk之外的普通低频数据：

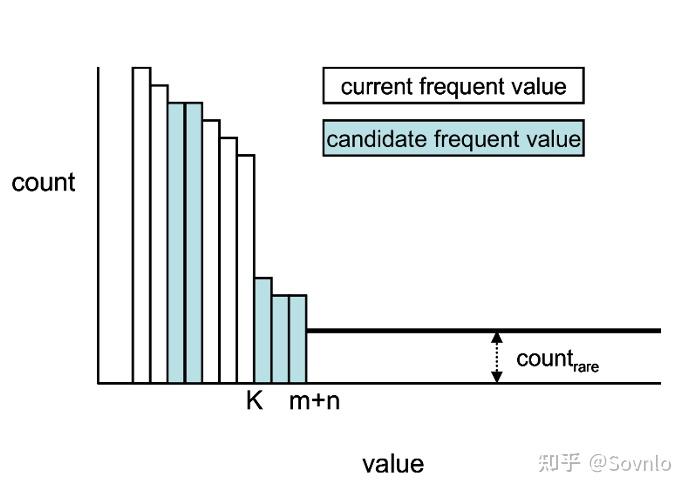
直接综合1，2，3中的数据，更新得到一个新的序列 。那么更新后的低频数据值： ，其中n<=K<=(m+n)。

随着时间的推移，feedback数据的增加，m+n可能会越来越大，因此需要限制top-K中K值的大小。由于feedback只提供了K范围内的准确数据，第K ~ m+n 之间的数值频率估计是存在误差的。总的误差值可以写为：

其中， 是区间（K+1, m+n）内的误差， 是区间 内的误差。从中我们可以得到这样一个trade-off的关系：K值越小，总的误差越高；K值越大，则feedback需要监控的top-k信息越多、开销越高。因此，我们应当尽可能地提升K值，并保证error(K)下降到一个可接受的范围。

问题定义：对于一个直方图，设第x个桶为 ，原高度为 ，根据feedback更新后的高度为 。现在我们得到一组feedback信息，将要更新N条数据到直方图中，每个桶x被更新的机会均等，其更新概率 满足概率分布： . 如果是范围更新，则概率分布是连续的，满足 。

现在我们得到了一组feedback，形式为：对于范围谓词 ，监控得到其基数，设为为 ；R与每个桶 的交集为 ，其高度为 。那么可以得到R整体与每个交集 的对应关系： ，

在图上形象表示下：

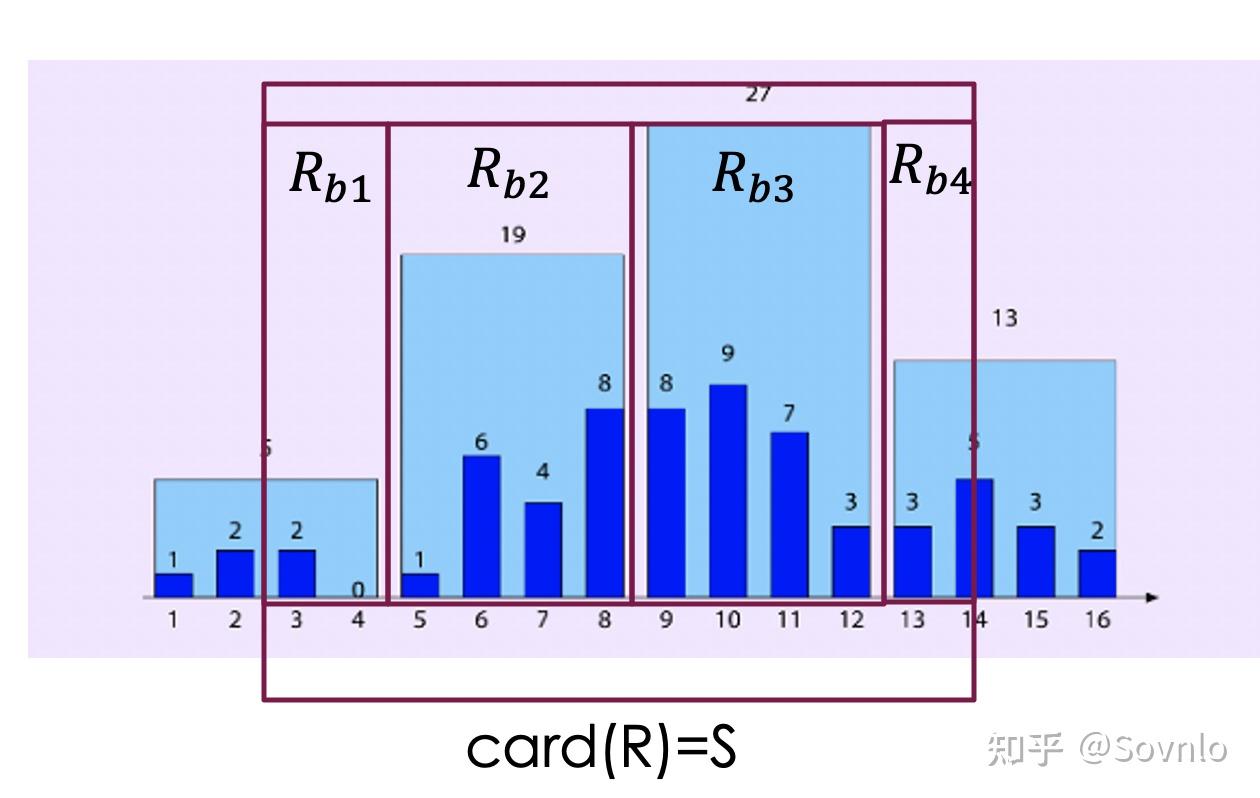
假设从feedback中，我们监测到了card(R)的真实值S： . 在这一条件下，某个桶x被R范围囊括，其更新后的高度，概率分布为 。利用贝叶斯公式推得： 。消除关联，得到：

其中，对于两概率相乘，由于左边符合概率分布 ，右边符合概率分布 ，两边相乘可以得到新的正态分布，均值为：

方差为

至此，我们得到了每个桶在确切的feedback监控信息下，更新高度的概率分布 ；据此可以依次对每个桶的高度进行更新，得到新的直方图。

多维直方图是用来表示多个关联列的直方图。我们给出问题定义：假设有d列，每列的最小值 ，最大值 ，多维直方图代表着空间 ；直方图上的每个桶 占据了空间中的一部分，这部分空间范围表示为 。

现在，假设我们从feedback中得到了一组谓词，和监测到的基数 其中每一个谓词q，代表着d个列上的谓词以and连词的形式结合到一起： 。举个形象的例子，对于Car表上的两个过滤谓词color='white'和make='Honda'，监控收集得到的反馈如下：

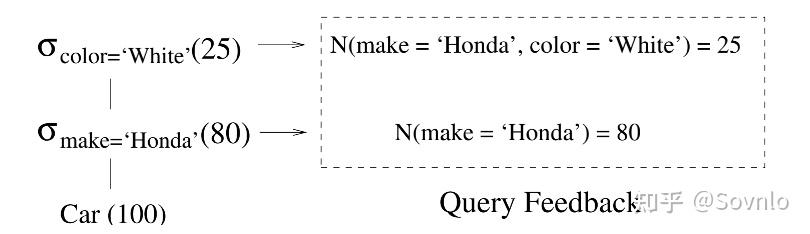
其中Car表总共100行，make 列包含’honda’, ‘bwm’两种值，可以映射为0, 1；color列包含’black’, ‘white’两种值，同样可以映射为0,1；不久，又从feedback监测到N(color=‘white’)=30。于是我们可以得到三个等式：

最开始我们假设直方图均匀分布。根据feedback逐步更新，我们得到：

会发现，根据feedback直接强行更新，会得到直方图上数据不一致的情况。需要设计一种算法，同时保证：

• 一致性：不违背表行数、feedback信息的一致性
• 均匀性：更新后的多维直方图保持均匀

我们来量化这一问题。根据Maximum-Entropy Principle，无约束情况下尽量保持数据分布均匀 (p代表概率分布)，其最大熵可以表示为 ，当数据连续时， 。

假设：谓词q，在多维直方图中覆盖的范围为R(q)，多维直方图的某个桶 ， 其覆盖的空间范围是 ，桶内数据总量为 ，vol代表某个空间的几何大小。从直方图中可以估算出谓词q的基数：

可以得到每个桶内，谓词q的概率分布:

带入maximum-entropy公式，得到

由于V(bi)和bi内部分布情况相互独立，可以消除转化得到

设某谓词q通过feedback得到的基数：

联立maximum-entropy，建立拉格朗日方程：

拉格朗日方程两边求导，并以e为底数化简两边，得到：

利用该方程的iterative scaling 解法，得到最终每个桶内的更新情况：

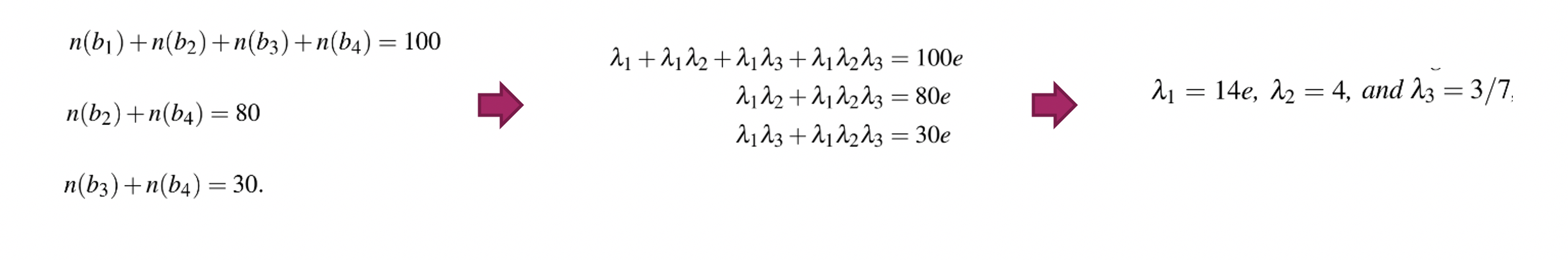
本文介绍了数据库统计信息的基本概念，以及如何通过feedback来修正统计信息，包括adjustment修正选择率、修正top-k直方图、修正一维直方图和多维直方图。

1. VLDB’01 LEO-DB2's learning optimizer

2. VLDB’04 Automated Statistics Collection in DB2 UDB

3. Hot DB’02 Course Project Reports: Hot Topics in Database Systems, Fall 2002, Statistical Analysis of Histograms

4. ICDE’06 ISOMER: Consistent Histogram Construction Using Query Feedback

5. VLDB’15 How Good Are Query Optimizers, Really?